AmpleGCG and Adaptive Dense-to-Sparse Constrained Optimization
We've now seen that optimizing an adversarial suffix for a specific LLM output can force the LLM to start its response with that output (and hopefully finish it). While the vanilla Greedy Coordinate Gradient (GCG) is perhaps the most canonical token-level jailbreak algorithm, it has a few key flaws. First, because it optimizes over discrete tokens, it is very inefficient. Consequently, both of the algorithms we cover in this writeup were at least partly created to improve token-level jailbreak efficiency. Second, because of the way the GCG loss is calculated, we oftentimes will end up with unsuccessful suffixes—we'll dive into why that happens first.
The Flaw in GCG's Loss
AmpleGCG (Liao & Sun, 2024) was created in part due to a critical observation made on the GCG optimization process: even if the adversarial suffix achieves a small loss on the target sequence, if the loss on the target sequence's first token is high, the model may start in "refusal mode" (e.g., by responding with "Sorry" rather than "Sure"). This unfortunately completely foils the adversarial attack.
This is a key idea, so we'll dive into it more formally as well. Once again, say we have an input sequence and a target response . Recall that the GCG loss is
Because the log of products is the sum of logs, we can rewrite the loss as
noticing that each token in the target sequence individually adds to the overall loss. Extracting the loss of the first token, we get
In seeing this equation, hopefully the flaw in the GCG loss becomes clear. Even if the loss over the full target sequence is low, the loss on the very first token of the target sequence () is what determines whether the LLM's response will start with, e.g., "Sure" or "Sorry". If the input sequence's loss on the first target token is high—even with a low average loss—the attack will likely fail. Unfortunately, the GCG loss does not factor in this observation.
It is for this reason, as pointed out by Daniel Paleka, that Confirm Labs found mellowmax to be a better GCG objective in practice (Straznickas et al., 2024).
AmpleGCG
Fig. 1
AmpleGCG (Liao & Sun, 2024)
Now that we understand why GCG's original objective is flawed, what (other than using mellowmax) can we do to improve it? Well, another finding of the AmpleGCG paper is that even though the GCG algorithm only returns one adversarial suffix, throughout the optimization process it generates thousands of other successful suffixes (which normally end up as discarded candidate suffixes) (Liao & Sun, 2024). When using all these suffixes to attack a model, we also see a great increase in attack success rate (ASR). Given that there are so many suffixes not returned by GCG, can we learn to generate them?
We can learn to generate them, and in fact, it's fairly easy to. Liao & Sun (2024) simply collected training pairs of (harmful query, adversarial suffix) by collecting the suffixes generated by GCG when optimizing for harmful query. They then fed these into Llama-2 for training and use a group beam search decoding scheme to encourage diversity in new suffix generation, dubbing the new model AmpleGCG.
At the time of its release, AmpleGCG was very effective at jailbreaking models, achieving an ASR of up to 99% on GPT-3.5 (although only 10% on GPT-4). Additionally, beacuse we now retrieve suffixes with a single forward pass in a model, AmpleGCG provides a great efficiency increase. It took AmpleGCG only 6 minutes to produce 200 suffixes for each of the 100 test queries, making it orders of magnitude more efficient than the original GCG algorithm.
Adaptive Dense-to-sparse Constrained Optimization
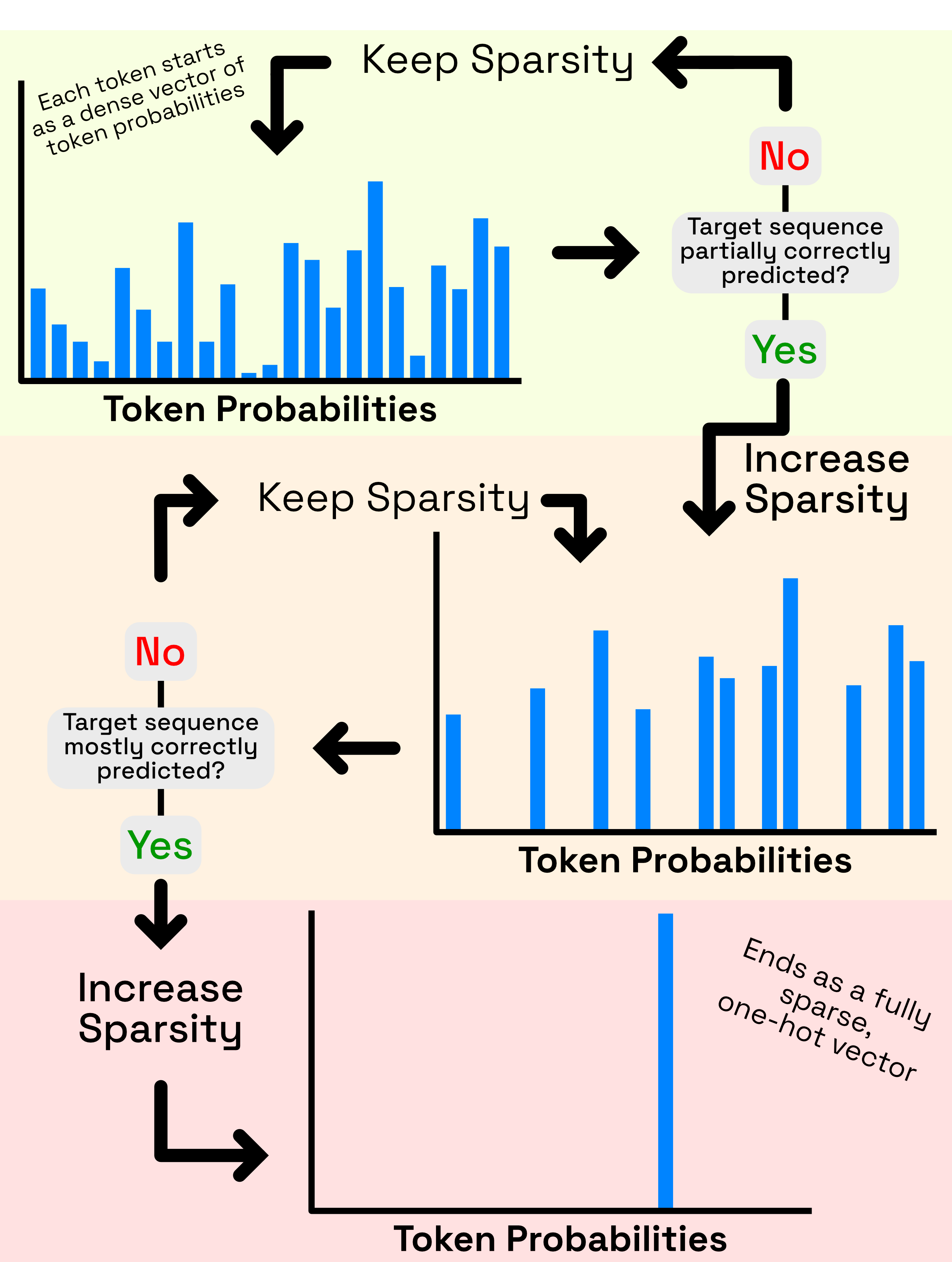
Fig. 2
Adaptive Dense-to-Sparse Constrained Optimization Attack (Hu et al., 2024)
Hu et al. (2024) also aims to improve the GCG algorithm, proposing an adaptive dense-to-sparse constrained optimization (ADC) attack. Their insight is that because GCG optimizes over discrete tokens, the process is rather inefficient compared to continuous optimizations. As a solution, they propose relaxing the discrete tokens into vectors in , then gradually constraining the optimization into a highly sparse space over time.
Notation, Notation, Notation
First, given a vocabulary of size , let denote the one-hot vector corresponding to vocabulary entry , with denoting the set of one-hot encodings for the vocabulary. Let our harmful prompt be denoted , our adversarial suffix , and our target response . The traditional GCG optimization goal is
where denotes concatenation.
The New Approach
Instead of performing the normal GCG optimization, we define a new relaxed continuous set of the probability space and optimize for
Pause. What did we just do? Well, recall that we no longer want to optimize in the one-hot vector set because it's quite slow. Instead, we turn each one-hot vector into a probability vector , where each entry of is non-negative () and the sum of all entries in is one (). Therefore, each vector in is no longer one-hot but represents a probability distribution over all the tokens, making optimization much more tractable.
The problem now is that we have a set of continuous vectors in that we'll eventually need to turn back into one-hot vectors to input into the LLM. We don't want to simply project the optimized vectors from to at the end, as projecting from dense to sparse vectors will likely greatly increase the optimization loss due to the distance between the dense and sparse vectors. Instead, at each optimization step, we convert to be -sparsity (meaning entries are nonzero), where
The idea behind this adaptive sparsity is that if all tokens in are mispredicted, will be large and there will be little sparsity constraint, whereas if all tokens are predicted correctly, , which gives a one-hot vector. In other words, we enforce a weaker sparsity constraint until we can find a good solution in our relaxed space .
To make the vectors a certain sparsity, we'll use the algorithm below:
The is added for numerical stability. The authors note that this isn't a projection algorithm and they use it basically just because it works. This happens a lot in machine learning.
Now, letting (our cross-entropy loss from before), here's the full algorithm:
As a quick warning, this algorithm is much more formal than the one presented in the original paper, but the concepts are all the same. We start with our user query, target response, and number of adversarial tokens. We initialize the adversarial tokens by taking the softmax output of a Gaussian distribution, then set our learning rate to 10 and momentum to 0.99. These steps are done to avoid local minima, and in practice ADC would also run in multiple streams to even further avoid local minima.
Inside the loop, we get the gradient of the adversarial suffix with respect to the loss, then use the gradient to update into according to our learning rate and momentum . Next, we get the target sparsity , sparsify the suffix into , and project the suffix onto to see if it successfully jailbreaks the model. If so, we stop early, and if not, we continue on.